2025.10.30

Overview

  1. 学习笔记
  2. 今日总结
  3. 摘录

学习笔记

概率

  1. 数据与数据表示
    1. 图表类型：
      1. 柱状图（Bar graph）
      2. 饼图（Pie Chart）
      3. 交叉表（Cross Table）：可以变成并排的簇状图（几个柱作为一个整体）或堆叠的分组条形图（一个柱上有几个不同的特性）
      4. 直方图（Histogram）
      5. 累积频率图（Ogive）：连接各区间上限累积百分比的线，展示累积频率分布
      6. 茎叶图（Stem and Leaf Plot）：同时展示数据的分布和原始值（中间的主干数据加上两边的枝干数据）
      7. 时间序列图（Time Series Plot）：横轴为时间，纵轴为序列值，展示数据随时间的变化趋势
      8. 散点图（Scatterplot）：观测两个定量变量的关系，需关注关联方向（正 / 负）、形式（线性 / 非线性）、强度（紧密 / 松散）
    2. 频率表
      1. 分类数据频率表：列出类别及对应数量（频率），相对频率表则列出百分比（比例）
        1. 频率表：
          舱位 数量
          头等舱（First） 324
          二等舱（Second） 285
          三等舱（Third） 710
          船员（Crew） 889
        2. 相对频率表
          舱位 百分比（%）
          头等舱（First） 14.67
          二等舱（Second） 12.91
          三等舱（Third） 32.16
          船员（Crew） 40.26
      2. 数值数据频率表：
        1. 构建规则：根据样本量n选择，如下表：
          样本量（n） 组数（k）
          <50 5-7
          50-100 7-8
          101-500 8-10
          501-1000 10-11
          1001-5000 11-14
          >5000 14-20
        2. 选择组宽：class width = (最大观测值 - 最小观测值) / 组数k （注意：需向上取整（根据数据小数位数））
        3. 组的要求：包含所有数据且不重叠，每个观测属于唯一一组
  2. 四种测量尺度
    尺度类型 核心特征 示例
    名义尺度（Nominal） 仅用于命名 / 标签，非定量值，无顺序和大小关系 欧洲国家、运动员 T 恤号码、性别、发色
    顺序尺度（Ordinal） 有顺序，非定量值，无法精确衡量差值 幸福感等级、服务满意度
    区间尺度（Interval） 定量，有顺序，可衡量差值，无 “真零”（零无实际意义），无法计算比率 摄氏温度（60℃与 50℃差值 = 80℃与 70℃差值 = 10℃，但 0℃不代表无温度）
    比率尺度（Ratio） 定量，有顺序，可衡量差值，有 “真零”（零代表无），可计算比率 体重（20kg 是 10kg 的 2 倍）、身高
  3. 分布描述
    1. 集中趋势测量（反映数据典型值）
      1. 均值（Mean，x̄）：算术平均，公式为 x̄ = (∑(i=1 到 n) xi) / (n - 1)
      2. 中位数（Median，m）：有序数据的中点，即第 50 百分位数
      3. 众数（Mode）：数据中出现频率最高的数值，可能有多个（如双峰、多峰分布）
    2. 离散程度测量（反映数据变异性）
      1. 范围（Range）：最大值与最小值的差值，公式为 Range = 最大观测值 - 最小观测值
      2. 四分位距（Interquartile Range，IQR）：上四分位数（Q3）与下四分位数（Q1）的差值，公式为 IQR = Q3 - Q1
        1. 计算Q1和Q3的规则：
          1. 若n为奇数：Q1是前(n+1/2)-1个数据的中位数，Q3是后(n+1/2)-1个数据的中位数
          2. 若n为偶数：Q1是前n/2个数据的中位数，Q1是后n/2个数据的中位数
      3. 方差（Variance，s^2）与标准差（Standard Deviation，s）：
        1. 方差：衡量数据与均值的偏离程度，样本方差公式为 s^2 = ∑(i=1 到 n) (xi - x̄)^2 / n-1 （分母用n-1是因为∑(xi - x̄) = 0，即仅n−1个偏差可自由变化）
        2. 标准差：方差的平方根，单位与原始数据一致，值越大说明数据越分散，越小则越集中
      4. 形状（反映数据分布形态）：
        1. 偏度（Skewness）：衡量分布的不对称性
          1. 负偏（Negatively skewed）：均值 < 中位数 < 众数，分布左侧长尾
          2. 正态（Normal，无偏）：均值 = 中位数 = 众数，分布对称
          3. 正偏（Positively skewed）：众数 < 中位数 < 均值，分布右侧长尾
        2. 众数数量：
          1. 单峰（Unimodal）：只有一个众数
          2. 双峰（Bimodal）：有两个众数
          3. 多峰（Multimodal）：有三个及以上众数
        3. 异常值（Outliers）：
          1. 定义：远离数据主体的观测值，可能由实验误差导致，有时需从数据集中剔除
          2. 判断标准：若观测值落在Q1 - 1.5IQR以下或Q3 + 1.5IQR以上，则可能为异常值
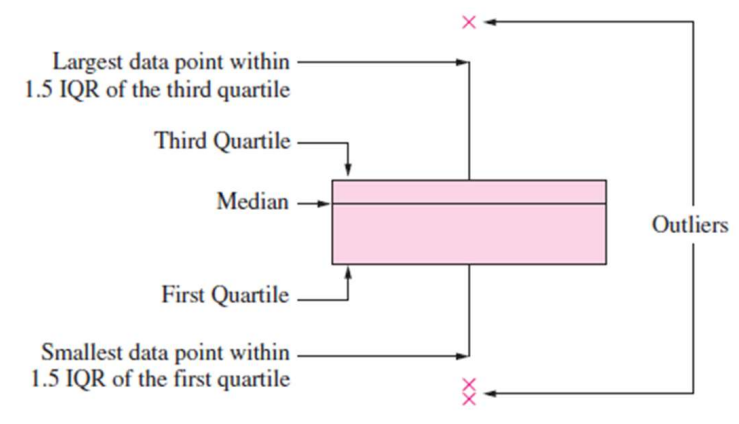
  4. 箱线图（Box-and-whisker plot）
    1. 定义：一种图形化展示数据分布的工具，呈现中位数、Q1、Q3及潜在异常值
    2. 组成部分：
      1. 箱体：从Q1延伸至Q3，箱内横线代表中位数
      2. 须（Whiskers）：从箱体两端延伸至 Q1 - 1.5IQR 和 Q3 + 1.5IQR 范围内的最小和最大数据点
      3. 异常值：超出须范围的数据点，单独标记
    3. 用途：作为诊断工具，直观观察数据分布的集中趋势、离散程度和异常值，非用于正式的异常值检验
      箱线图
  5. 随机变量及其性质
    1. 随机变量定义：设随机实验的样本空间为S，若对每个样本点 s∈S，都有唯一的实数X(s)与之对应，则称X=X(s)为随机变量
      1. 示例：抛 10 次硬币实验，样本空间S = {s|s是十次正反面的序列}，定义随机变量X(s)为序列中正面出现的次数，则X(s)的取值范围为Rx = {1，2，···，10}
    2. 随机变量类型
      1. 离散随机变量（Discrete Random Variable）：取值为有限个或可列无限个
      2. 连续随机变量（Continuous Random Variable）：取值充满某个区间
    3. 随机变量的特征
      1. 均值（期望，Mean/Expectation，μ）：
        1. 离散随机变量：μ = E[X] = ∑x xp(x)，其中p(x) = P(X = x)为概率质量函数
        2. 连续随机变量：μ = E[X] = ∫(负无穷 到 正无穷) xf(x)dx，其中f(x)为概率密度函数，且∫(负无穷 到 正无穷) f(x)dx = 1
      2. 中位数（Median，m）：
        1. 离散随机变量：满足 P(X ≤ m) ≥ 1/2 且 P(X ≥ m) ≥ 1/2 的数值
        2. 连续随机变量：概率密度函数下面积被x=m分为两部分，每部分面积为1/2，即 ∫(负无穷 到 m) f(x)dx = 1/2
      3. 众数（Mode）：概率密度函数（或概率质量函数）的局部最大值点，可能有多个
      4. 方差（Variance，σ^2）：衡量随机变量取值与均值的偏离程度，公式为σ^2 = E[(X−μ)^2]，其中：
        1. 离散随机变量：σ^2 = ∑x (x-μ)^2p(x)
        2. 连续随机变量：σ^2 = ∫(负无穷 到 正无穷) (x-μ)^f(x)dx
      5. 累积分布函数（Cumulative Distribution Function，CDF，F(x)）：F(x) = P(X≤x)，其中：
        1. 离散随机变量：F(x) = ∑(t≤x) p(t)
        2. 离散随机变量：F(x) = ∫(负无穷 到 x) f(t)dt
  6. 抽样分布
    1. 随机样本：设X1，X2，···， Xn是相互独立的随机变量，且每个Xi都与总体X具有相同的概率密度函数f(x)，则称X1，X2，···， Xn为来自总体X的容量为n的随机样本。随机样本的联合概率密度函数为 f(x1，x2，···，xn) = f(x1)f(x2)···f(xn)
    2. 统计量：
      1. 定义：设X1，X2，···， Xn是来自总体的随机样本，若样本的函数T = T(X1，X2，···， Xn)不含任何未知参数，则称T为统计量
      2. 常见统计量：
        1. 样本均值：ˉX= 1/n ∑(i=1 到 n) Xi（对应观测样本的 x̄ = 1/n ∑(i=1 到 n) xi是具体数值，而ˉX是随机变量）
        2. 样本方差：S^2 = 1/(n-1) ∑(i=1 到 n) (Xi - ˉX)^2（对应观测样本的 s^2 = 1/(n-1) ∑(i=1 到 n) (xi - x̄)^2是具体数值，而S^2是随机变量）
      3. 抽样分布定义：统计量的概率分布称为抽样分布，它描述了统计量的取值规律，是进行统计推断（如估计总体参数、检验假设）的重要依据，通过抽样分布可将样本信息与总体参数关联起来
  7. 样本均值的抽样分布
    1. 核心结论：
      1. 期望：样本均值的期望等于总体均值，即 E[X] = μ
      2. 方差：样本均值的方差等于总体方差除以样本量，即 Var(ˉX) = σ^2/n（若总体方差为σ^2)
    2. 两种情况的抽样分布形态：
      总体分布情况 样本均值ˉX的抽样分布 适用条件
      总体服从正态分布 (X ∼ N(μ，σ^2)) X ∼ N(μ，σ^2/n) 无论样本量n大小，均成立
      总体分布未知（但总体均值μ、方差σ^2有限） 当n足够大时，近似 X ∼ N(μ，σ^2/n) 中心极限定理（CLT），通常 n≥30 时近似效果好；若n<30，需总体分布接近正态
    3. 示例：
      1. 已知：某大学学生平均年龄μ=22.3岁，标准差σ=4岁（方差σ^2=16），随机抽取n=64名学生
      2. 求：样本平均年龄大于23岁的概率 P(ˉX > 23)
      3. 解：因 n=64 ≥ 30，由CLT，X ∼ N(μ = 22.3，σ^2/n = 16/64) = N(22.3，0.25)标准化得 Z = (ˉX - μ) / √σ ∼ N(0，1)，则 P(ˉX > 23) = P(Z > (23-22.3)/√0.25) = P(Z > 1.40)。查标准正态分布表，P(Z ≤ 1.40) = 0.9192，所以P(Z > 1.40) = 1 - 0.9192 = 0.0808
  8. 中心极限定理（CLT）的用途
    1. 获取样本均值的抽样分布：基于总体参数 (μ，σ^2)和样本量n，确定ˉX的分布形态（近似正态分布），为后续统计计算奠定基础
    2. 推断未知总体均值μ：
      1. 假设检验：判断样本均值x̄是否支持对μ的某个假设（如“μ = μ0”）
      2. 估计：通过样本均值及抽样分布，给出μ的估计区间（如置信区间）
      3. 质量控制：监测生产过程中产品指标的均值是否在合理范围内，判断过程是否稳定
  9. 两均值差的抽样分布（ˉX1 - ˉX2）
    1. 定理：设从两个总体中分别抽取独立样本：
      样本1：容量n1，来自均值μ1，方差σ^2(1)的总体
      样本2：容量n2，来自均值μ2，方差σ^2(2)的总体
      则当n1和n2足够大时（通常≥30），或两个总体均服从正态分布时，两样本均值差 ˉX1 - ˉX2 近似服从正态分布：ˉX1 - ˉX2 ∼ N(μ1-μ2，σ^2(1)/n1 + σ^2(2)/n2) （注意加减号）
  10. X^2分布
    1. 定义：设X1，X2，···，Xn是来自正态总体N(μ，σ^2)的随机样本，S^2为样本方差，则统计量 X^2 = (n-1)S^2 / σ^2，服从自由度为 v = n-1 的X^2分布，记为 X^2 ∼ X^2(v)
    2. 形态：
      1. 取值范围：X^2 ≥ 0（非负）
      2. 自由度影响：自由度v越小，分布越偏右；v越大，分布越接近正态分布
      3. 分位数：用 X^2(a)(v) 表示自由度为v的X^2分布中，右侧面积为a的分位数（如v=7时，X^2(0.05)(7) = 14.067，X^2(0.95)(7) = 2.167）
      4. 区间概率：如 95% 的X^2值落在X^2(0.975)(v)与X^2(0.025)(v)之间，若X^2值超出此范围，可能表明假设的总体方差σ^2不合理
    3. 用途：主要用于统计推断，核心是检验 “观测数据与预期数据的差异是否由随机因素导致”，具体应用包括：
      1. 总体方差的区间估计和假设检验（如判断总体方差是否等于某个假设值）
      2. 拟合优度检验（检验观测数据是否符合某一理论分布，如正态分布、二项分布）
      3. 独立性检验（检验两个分类变量是否独立）
  11. t分布（Student t -Distribution）
    1. 定义：
      1. 基础定义：设 Z ∼ N(0，1)（标准正态分布），V ∼ X^2(v)（自由度v的X^2分布），且Z与V独立，则随机变量 T = Z / √(V/v) 服从自由度为v的t分布，记作 T ∼ t(v)
      2. 推论（样本均值相关）：设 X1，X2，···，Xn 是来自正态总体N(μ，σ^2)的随机样本，ˉX为样本均值，S^2为样本方差，则统计量 T = (ˉX - μ) / (S/√n)，服从自由度为 v = n-1 的t分布
    2. 形态：
      1. 对称性：钟形，关于t=0对称（与标准正态分布类似）
      2. 方差特性：方差 = v / v-2 (v>2)，大于1，故比标准正态分布更分散（尾部更粗）
      3. 自由度影响：自由度v越大，t分布越接近标准正态分布（v趋近于无穷时，t分布趋近于N(0,1)）
      4. 分位数：用ta(v)表示自由度为v的t分布中，右侧面积为a的分位数，由对称性得t1-a(v) = -ta(v)
    3. 用途：
      1. 核心场景：总体方差σ^2未知时的统计推断，具体包括：
        1. 总体均值μ的区间估计和假设检验（如样本量较小时，用S替代σ，用 t 分布而非正态分布）
        2. 两独立样本均值差的检验（当两总体方差未知且可能相等或不等时，用t分布或近似t分布）
        3. 配对样本均值差的检验（如同一组对象前后两次测量的均值差检验）
      2. 注意事项：
        1. 使用 t 分布的前提是总体服从正态分布（或样本量较大时，由CLT近似正态，但t分布的使用与CLT无直接关联）
        2. 若总体不服从正态且样本量小（n<30），则t分布的近似效果差，不宜使用
  12. F分布
    1. 定义
      1. 基础定义：设 U ∼ X^2(v1)（自由度v1的X^2分布），V ∼ X^2(v2)（自由度v2的X^2分布），且U与V独立，则随机变量 F = (U/v1)/(V/v2) 服从自由度为(v1，v2)的F分布，记为 F ∼ F(v1，v2)，其中v1为分子自由度，v2为分母自由度
      2. 推论（样本方差相关）：设 S^2(1) 是来自正态总体 N(μ1，σ^2(1)) 的样本（容量n1）的方差，S^2(2) 是来自正态总体 N(μ2，σ^2(2)) 的样本（容量n2）的方差，且两样本独立，则统计量 F = (S^2(1)/σ^2(1)) / (S^2(2)/σ^2(2)) = σ^2(2)S^2(1) / σ^2(1)S^2(2) 服从自由度为(v1 = n1 - 1，v2 = n2 - 1)的F分布，
    2. 形态
      1. 取值范围：F≥0（非负）
      2. 自由度影响：分布形态由分子自由度v1和分母自由度v2共同决定，通常为右偏分布，v1和v2越大，分布越接近正态分布
      3. 分位数：用fa(v1，v2)表示自由度为(v1，v2)的F分布中，右侧面积为a的分位数
      4. 分位数关系：fa(v1，v2) = 1 / (f1-a(v2，v1))，用于计算低尾分位数
    3. 用途：
      1. 核心场景：方差分析（Analysis of Variance，ANOVA），用于检验多个总体均值是否相等，具体包括：
        1. 单因素方差分析（如检验三种油漆的平均干燥时间是否相等）：通过比较 “组间方差”（样本均值间的变异）与 “组内方差”（样本内部的变异）的比值（F统计量），判断均值是否存在显著差异
        2. 两总体方差的比较：检验两个正态总体的方差是否相等（如判断两样本的方差是否齐性，为两样本均值检验选择方法）
        3. 多因素方差分析：分析多个因素对因变量的影响及因素间的交互作用
  13. 本章关键问题：
    1. 在数据分布描述中，异常值的判断标准是什么？为什么在计算样本方差时，分母使用n−1而非n？
      1. 异常值判断标准：若某个观测值落在 Q1−1.5IQR以下或Q3+1.5IQR以上，则该观测值可能为异常值
      2. 样本方差分母用n−1的原因：为了实现无偏估计，由于样本均值x̄是通过样本数据计算得出的，存在 “自由度损失” —— ∑(i=1 到 n) (xi - x̄) = 0，即n个偏差中只有n−1个是独立的若用
    2. 心极限定理（CLT）的核心内容是什么？其在样本均值抽样分布和两均值差抽样分布中有哪些具体应用？
      1. 中心极限定理（CLT）核心内容：设总体的均值为μ、方差为σ^2（有限），从该总体中抽取容量为n的随机样本，当n足够大时（通常n≥30），样本均值ˉX的抽样分布近似服从均值为μ，方差为σ^2/n的正态分布（即近似 ˉX ∼ N(μ，σ^2/n)）且该近似效果与总体原始分布无关（即使总体非正态，只要n足够大，样本均值仍近似正态）
      2. 在样本均值抽样分布中的应用：
        1. 当总体分布未知时，若n≥30，可通过CLT认为ˉX近似正态，进而计算与样本均值相关的概率
        2. 当n<30时，若总体分布接近正态CLT的近似效果仍可接受；若总体严重非正态，则需增大样本量以满足CLT条件
      3. CLT 可推广到两独立样本场景
    3. X^2分布、T分布、F分布的核心用途有何差异？分别适用于哪些统计推断场景？
      1. X^2分布、T分布、F分布的核心用途及适用场景存在显著差异，具体如下表所示：
        分布类型 核心用途 适用场景示例
        X^2分布 围绕方差与数据拟合程度展开，用于检验 “观测数据与预期数据的差异是否由随机因素导致” 1. 总体方差推断：总体方差σ^2的区间估计和假设检验（如判断汽车电池寿命的标准差是否为 1 年）
        2. 拟合优度检验：检验观测数据是否符合某一理论分布（如检验学生成绩是否服从正态分布）
        3. 独立性检验：检验两个分类变量是否独立（如检验 “性别” 与 “是否购买某产品” 是否独立）
        T分布 围绕总体方差未知时的均值推断展开，解决 “总体方差σ^2未知，无法使用正态分布” 的问题 1. 单总体均值推断：总体方差未知时，总体均值μ的区间估计和假设检验（如样本量较小时，检验化工过程的产量均值是否为 500g/ml）
        2. 两样本均值差推断：两总体方差未知时，检验两总体均值是否相等（如检验两种药物的疗效均值是否有差异）
        3. 配对样本推断：检验配对数据的均值差（如检验同一组患者用药前后的血压均值差）
        F分布 围绕方差比值与多总体均值比较展开，核心是 “通过方差比值判断差异是否显著” 1. 两总体方差比较：检验两个正态总体的方差是否相等（如判断两批产品的质量波动是否一致，即方差齐性检验）
        2. 方差分析（ANOVA）：检验多个总体的均值是否相等（如检验三种不同品牌油漆的平均干燥时间是否有差异）
        3. 多因素方差分析：分析多个因素对因变量的影响及因素间的交互作用（如分析 “温度”“压力” 对产品产量的影响）
      2. 三者的核心差异在于：X^2分布聚焦 “方差与拟合度”，T分布聚焦 “方差未知时的均值”，F分布聚焦 “方差比值与多均值比较”，分别对应统计推断中不同维度的问题

今日总结

  1. 今天在记笔记时要加入表格，发现：
    1. 为了避免序号被打乱，要通过缩进确保表格属于上一级列表项
    2. 若需要在表格中加入序列需要使用<br>标签进行换行
  2. 今天在记笔记时要插入图片，步骤如下：
    1. 在source文件夹里创建一个images文件夹用于存放图片
    2. 在Markdown文件中用语法：！\[图片描述]\[/images/图片名]
    3. 注意：此方法只能在发布出来的博客中看见图片
    4. 过程中在终端中下载了安装 hexo-asset-img 插件
  3. 今天看见Stela在跑步，和她约了下次一起跑步
  4. 英语口语学习
  5. 今天的网球活动感觉打的越来越好了

摘录

  1. 管理情绪主要包括三个方面的内容：一是认识自己的情绪；二是疏解自己的情绪；三是适当表达自己的情绪。
  2. 脱困四问：
    1. Emotion：我正处于何种情绪里？这种情绪的程度如何？
    2. Event：我为什么产生这样的情绪？（注意：需要客观真实看待所发生的事情，不能带有主观倾向）
    3. Target：我的初衷是什么？
    4. Action：接下来我该怎么做？我可以做些什么？
  3. 生活的本质在于追求快乐，而让自己的人生变得快乐的途径有两种：不断地发现有限生命中的快乐时光，并增加它；发现那些令自己不快乐的时光，并尽可能减少它。 —— 亚里士多德
  4. 两弊相衡取其轻，两利相权取其重