Overview
- 今日学习笔记
- 句子摘录
- 昨天和今天的总结
学习笔记
概率
- 随机变量(Random Variables)
- Definition:设样本空间为 Ω,随机变量 X 是定义在 Ω 上、取值于实数集ℝ的函数,即X: Ω→R,X(ω) 表示对样本点 ω 的赋值
- Example:掷骰子(Ω={1,2,3,4,5,6}),X(1-3)=1(赢1元),X(4-6)=-1(输1元),刻画玩家收益
- 概率表示:事件 “X 取 x 值” 即 {ω∈Ω | X(ω)=x},概率简化记为P(X=x),且所有可能取值概率和为 1(∑P (X=x)=1)
- 离散型随机变量及其分布(Discrete Random Variables and Distributions)
- Definition:取值为有限个或可列个,且每个取值有其概率,不可能的取值的概率为0.
- 概率质量函数(probability mass function (pmf)):f(x)满足:
- f(x)≥0
- ∑f (x)=1(所有可能 x 求和)
- 分布函数(distribution function):F(x)=P(X≤x)=∑(x_j≤x) f(x_j),其具有性质:
- lim(x→-∞)F(x)=0
- lim(x→+∞)F(x)=1
- 非递减
- 0≤F(x)≤1
- 离散型随机变量的平均数或期望(mean or expectation or expected value):μ = E[X] = ∑_j x_j f(x_j), j = 1,2,…,n(f是X的pmf,x_j是X的可能取值)
- 进一步推导出:E[g(X)] = ∑_j g(x_j) f(x_j), j = 1,2,…,n
- 离散型随机变量的方差(variance):σ^2 = Var(X) = E[(X - E(X))^2] = ∑_j (x_j - E(X))^2 f(j_x)
- 方差提供𝑋围绕其均值E𝑋的离散程度的度量,其总是非负的
- 标准差(standard deviation):σ = √Var(X)
- 均值和方差的性质:
- 设𝑋为随机变量,我们考虑𝑋的线性函数:𝑌 = 𝑎𝑋 + b,a,b ∈ R 其具有性质:
- E(Y) = aE(X) + b
- Var(Y) = a^2Var(X)
- 可以用以下公式表示随机变量𝑋的方差:
Var(X) = E(X^2) - E(X)^2
- 设𝑋为随机变量,我们考虑𝑋的线性函数:𝑌 = 𝑎𝑋 + b,a,b ∈ R 其具有性质:
- 伯努利分布(Bernoulli Distribution):
- Definition:随机变量X只能取值1或0,其概率分别为 p ∈ (0,1),q(:= 1-p)
- 可能取值:1,2
- pmf:P(X=1) = p,P(X=0) = 1-p
- E (X):p
- Var (X):p(1-p)
- 二项分布(Binomial Distribution):𝑋 ∼ Bin(n,p),n∈ℕ, p∈(0,1))
- Definition:n次独立试验中成功次数的离散概率分布,每个试验的成功概率为𝑝
- 可能取值:0,1,…,n
- pmf:P(X=k) = C(n,k) p^k (1-p)^(n-k) (
C(n,k) = n! / k! (n-k)!) - E (X):np
- Var (X):np(1-p)
- 泊松分布(Poisson Distribution):𝑋 ∼ Poi(λ),λ>0
- Definition:泊松分布是一种离散概率分布,用于计算在固定时间或空间间隔内,以已知平均发生率且独立于上次事件发生时间的事件发生次数的概率。
- 可能取值:0,1,2,…
- pmf:P(X=k) = e^(-λ) λ^k / k!
- E (X):λ
- Var (X):λ
- 注意:问题中给出的速率可能不是所需区间内的𝜆值!我们需要对其进行放大或缩小,以获得正确的𝜆值。(如给了一周的速率为𝜆,要计算两周的间隔则速率为2𝜆)
- 几何分布(Geometric Distribution):𝑋 ∼ Geo(p),p∈(0,1)
- Definition:经过X次试验才得到成功的结果
- 可能取值:1,2,3,…(不能为0)
- pmf:P(X=k) = p (1-p)^(k-1)
- E (X):1/p
- Var (X):(1-p)/p²
- 连续型随机变量及其分布(Continuous Random Variables and Distributions)
- Definition:取值能充满某个区间(或多个区间),且其取任何单个特定值的概率均为 0 的随机变量
- 概率密度函数(probability density function(pdf)):f(x)满足:
- f(x)≥0
- ∫(-∞到+∞) f(x) dx = 1
- 分布函数(Distribution Function):F(x) = P(X≤x) = ∫(-∞到 x) f(t) dt,具有性质:
- lim(x→-∞)F(x)=0
- lim(x→+∞)F(x)=1
- 𝐹可微(因此连续),是非递减函数
- 0 ≤ 𝐹(x)≤ 1
- f(x) = F’(x)
- 连续随机变量的均值(Mean of Continuous Random Variable):μ = E[x] = ∫(-∞到+∞) xf(x) dx ,(f(x)是pdf)
- 进一步推导出:E[g(X)] = ∫(-∞到+∞) g(x)f(x) dx
- 连续随机变量的方差(Variance of Continuous Random Variable):σ^2 = Var(X) = E[(X - E(X))^2] = ∫(-∞到+∞) (x - E(X))^2 f(x) dx
- 均值和方差的性质:
- 设𝑋为随机变量,我们考虑𝑋的线性函数:𝑌 = 𝑎𝑋 + b,a,b ∈ R 其具有性质:
- E(Y) = aE(X) + b
- Var(Y) = a^2Var(X)
- 我们可以用以下公式表示随机变量𝑋的方差:
Var(X) = E(X^2) - E(X)^2
- 设𝑋为随机变量,我们考虑𝑋的线性函数:𝑌 = 𝑎𝑋 + b,a,b ∈ R 其具有性质:
- 均匀分布(Uniform Distribution):X ~ U(a,b), a<b
- pdf:f(x) = 1/(b-a)(a<x<b),否则 0
- E(X):(a+b)/2
- Var(X):(b-a)²/12
- 指数分布(Exponential Distribution):X ~ Exp(λ),λ>0
- pdf:f(x) = λe^(-λx)(x≥0),否则 0
- E(X):1/λ
- Var(X):1/λ²
- 注意:指数分布常被用作描述特定事件发生前时间长度的分布(eg:从现在开始到发生地震的时间长度)
- 正态分布(Normal Distribution):X ~ N(μ,σ²),μ∈R, σ>0
- pdf:f(x)=1/(√(2π)σ)e^(-(x-μ)²/(2σ²))
- E(X):μ
- Var(X):σ²
- 正态分布关键特性:
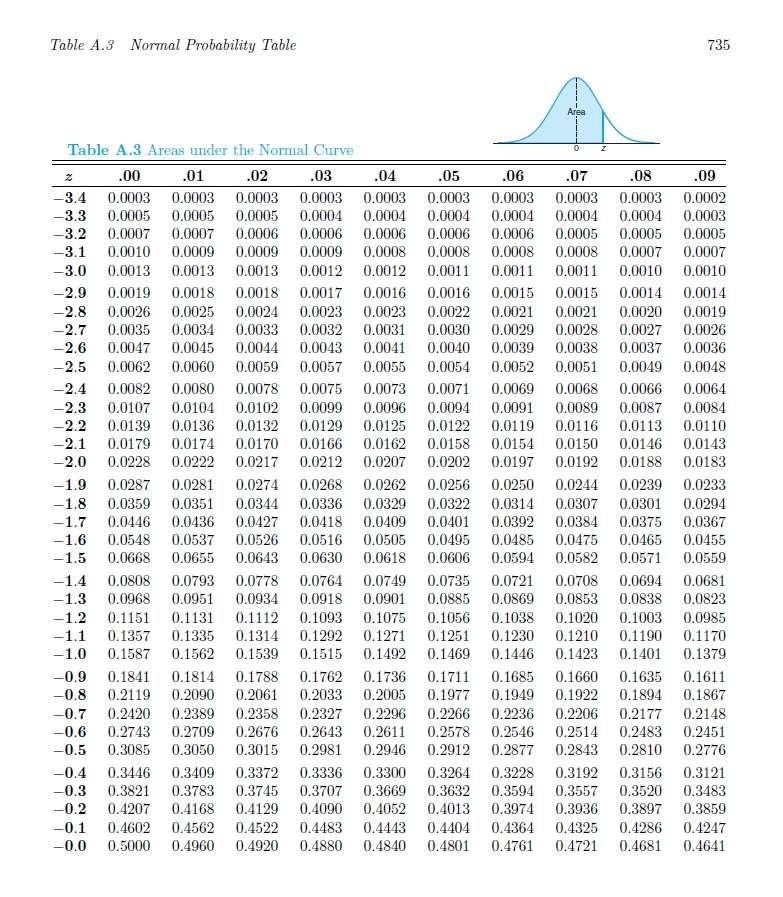
- 标准化:若 X
N (μ,σ²),则Z=(X-μ)/σN(0,1)(标准正态分布),通过标准正态表查概率 - 3σ 原则:P(μ-σ<X<μ+σ)≈68.27%,P(μ-2σ<X<μ+2σ)≈95.45%,P(μ-3σ<X<μ+3σ)≈99.73%
- 标准化:若 X
- 解题步骤:
将X转换成Z的范围- 用上限减去下限
- 查找对应值带入计算
- 二维分布(2D Distributions)
- 二维离散分布(Discrete 2D Distributions)
- 联合 pmf:f (x_i,y_j)=P (X=x_i,Y=y_j),满足∑∑f (x_i,y_j)=1
- 边际 pmf:f_X (x_i)=∑(j) f (x_i,y_j)(对 Y 求和),f_Y (y_j)=∑(i) f (x_i,y_j)(对 X 求和)
- 分布函数:F(x,y) = ∑(x_i<=x)∑(y_i<=y) f(x_i,y_j)
- ∑i∑j f(x_i,y_j) = 1
- X的边际分布:f(x) = ∑j f(x,y_j)
- Y的边际分布:f(y) = ∑i f(x_i,y)
- 如果X和Y相互独立:f(x_i|y_j) = f(x_i) or f(x_i,y_j) = f(x_i)f(y_j)
- 期望值:E(g(X,Y)) = ∑i∑j g(x_i,y_j) f(x_i,y_j)
- 二维连续分布(Continuous 2D Distributions)
- 联合 pdf:f (x,y)≥0,∫(-∞到 +∞)∫(-∞到 +∞) f (x,y)dxdy = 1
- 边际 pdf:f_X (x)=∫(-∞到 +∞) f (x,y) dy,f_Y (y)=∫(-∞到 +∞) f (x,y) dx
- 分布函数:F(x,y) = ∫(Y<=y)∫(X<=x) f(X,Y)dXdY
- X的边际分布:f(x) = ∫(-∞到 +∞) f(x,y)dy
- Y的边际分布:f(y) = ∫(-∞到 +∞) f(x,y)dx
- 如果X和Y相互独立:f(x|y) = f(x) or f(x,y) = f(x)f(y)
- 期望值:E(g(X,Y)) = ∫(-∞到 +∞)∫(-∞到 +∞) g(x,y)f(x,y)dxdy
- P(a<=X<=b,c<=Y<=d) = ∫(c到d)∫(a到b) f(x,y)dxdy
- 条件概率描述 “在Y满足某条件时,X发生的概率”,分三类情况:
- P(X<=x|Y<=y) = P(X<=x|Y<=y) / P(Y<=y) = F(x,y) / F(y)
- P(X<=x|Y=y) = ∫(X<=x) f(x|y)dx = ∫(X<=x) f(x,y)/f(y) dx
- P(X<=x|Y>=y) = P(X<=x|Y>=y) / P(Y>=y) = ∫(Y>=y)∫(X<=x) f(x,y) dxdy / ∫(Y>=y) f(y) dy
- 二维离散分布(Discrete 2D Distributions)
- 数字特征与相关性
- 均值的运算性质
- 求和定理(Sum of Means):对任意随机变量 X₁,X₂,…,Xₙ(离散/连续、独立/依赖),E(X₁+X₂+…+Xₙ) = E(X₁)+E(X₂)+…+E(Xₙ)
- 乘积定理(Product of Means):仅当X₁,X₂,…,Xₙ独立时(每个随机变量的取值都不会对其他随机变量的取值概率产生影响)(离散、连续都适用),E(X₁X₂…Xₙ)=E(X₁)E(X₂)…E(Xₙ)
- 独立性与不相关性
- 独立性(independent):X与Y独立 -> f(x,y) = f(x)f(y)(离散pmf / 连续pdf)
- 不相关性(uncorrelated):X与Y不相关 -> E(XY) = E(X)E(Y) -> Cov(X,Y) = 0 -> ρ(X,Y) = 0
- 关系:独立→不相关,但不相关≠独立
- 协方差与相关系数
- 协方差(Covariance):Cov(X,Y) = E[(X-μ_X)(Y-μ_Y)] = E(XY) - E(X)E(Y),反映X与Y“同增同减” 趋势(Cov>0:正相关,Cov<0:负相关)
- 相关系数(Correlation):ρ(X,Y)=Cov (X,Y)/(σ_Xσ_Y),ρ∈[-1,1],是无量纲的线性关联度量
- ρ=1:完全正线性相关
- ρ=-1:完全负线性相关
- ρ=0:无线性相关
- 双变量正态分布
- 定义:X与Y联合正态 -> 对任意 a,b∈R,aX+bY 正态分布
- 关键性质:若 X 与 Y 联合正态且不相关(ρ=0),则X与Y独立(区别于一般随机变量)
- 均值的运算性质
摘录
- 我们一步一步走下去,踏踏实实地去走,永不抗拒生命交给我们的重负,才是一个勇者。到了蓦然回首的那一瞬间,生命必然给我们公平的答案和又一次乍喜的心情,那时的山和水,又恢复成最初单纯的样子,而人生走过的是多么美好的一个秋天。 – 三毛
昨日总结
昨天参加了本学期第一次飞盘活动,感觉是开学以来参与感最强的一次活动了,既能够充分运动,也可以认识很多朋友(争取吧)
今日总结
- 今天完成了概率课程的提交作业,整体写下来还是比较容易的,就是中途发现还是有些地方想得过于复杂了
- 读书一章
- 复习完全部单词
- 本周第二次网球活动